Feb 3, 2018

Protection against over voltage Q & A- PART-A

Protection against over voltage

1. Why protection of transmission line important?

It is essential for electrical power engineers to reduce the number of outages and preserve the
continuity of service and electric supply.

2. What are the causes of over voltages in electric system?

 External Cause – Lightning
 Internal Cause – Switching

3. What are the causes of power frequency over voltages?

Concept of Stepper motors

Stepper motors

A stepper motor is a "digital" version of the electric motor. The rotor moves in discrete steps as commanded, rather than rotating continuously like a conventional motor. When stopped but energized, a stepper (short for stepper motor) holds its load steady with a holding torque. Wide spread acceptance of the stepper motor within the last two decades was driven by the ascendancy of digital electronics. Modern solid state driver electronics was a key to its success. And, microprocessors readily interface to stepper motor driver circuits.

AC Bridge Circuits

As we saw with DC measurement circuits, the circuit configuration known as a bridge can be a very useful way to measure unknown values of resistance. This is true with AC as well, and we can apply the very same principle to the accurate measurement of unknown impedance. To review, the bridge circuit works as a pair of two-component voltage dividers connected across the same source voltage, with a null-detector meter movement connected between them to indicate a condition of “balance” at zero volts: (Figure below)

A balanced bridge shows a “null”, or minimum reading, on the indicator.

Interview questions with answer

Q:Why syn. generators are used for the production of electricity?

Gas Turbine Power Plant

An internal combustion engine in which expanding gases from the combustion

Long and Short Transmission Lines-Transmission line PART-E

Long and Short Transmission Lines

In DC and low-frequency AC circuits, the characteristic impedance of parallel wires is usually ignored. This includes the use of coaxial cables in instrument circuits, often employed to protect weak voltage signals from being corrupted by induced "noise" caused by stray electric and magnetic fields. This is due to the relatively short time spans in which reflections take place in the line, as compared to the period of the waveform or pulses of the significant signals in the circuit. As we saw in the last section, if a transmission line is connected to a DC voltage source, it will behave as a resistor equal in value to the line's characteristic impedance only for as long as it takes the incident pulse to reach the end of the line and return as a reflected pulse, back to the source. After that time (a brief 16.292 μs for the mile-long coaxial cable of the last example), the source "sees" only the terminating impedance, whatever that may be.

If the circuit in question handles low-frequency AC power, such short time delays introduced by a transmission line between when the AC source outputs a voltage peak and when the source "sees" that peak loaded by the terminating impedance (round-trip time for the incident wave to reach the line's end and reflect back to the source) are of little consequence. Even though we know that signal magnitudes along the line's length are not equal at any given time due to signal propagation at (nearly) the speed of light, the actual phase difference between start-of-line and end-of-line signals is negligible, because line-length propagation occur within a very small fraction of the AC waveform's period. For all practical purposes, we can say that voltage along all respective points on a low-frequency, two-conductor line are equal and in-phase with each other at any given point in time.

In these cases, we can say that the transmission lines in question are electrically short, because their propagation effects are much quicker than the periods of the conducted signals. By contrast, an electrically long line is one where the propagation time is a large fraction or even a multiple of the signal period. A "long" line is generally considered to be one where the source's signal waveform completes at least a quarter-cycle (90o of "rotation") before the incident signal reaches line's end. Up until this chapter in the Lessons In Electric Circuits book series, all connecting lines were assumed to be electrically short.

To put this into perspective, we need to express the distance traveled by a voltage or current signal along a transmission line in relation to its source frequency. An AC waveform with a frequency of 60 Hz completes one cycle in 16.66 ms. At light speed (186,000 m/s), this equates to a distance of 3100 miles that a voltage or current signal will propagate in that time. If the velocity factor of the transmission line is less than 1, the propagation velocity will be less than 186,000 miles per second, and the distance less by the same factor. But even if we used the coaxial cable's velocity factor from the last example (0.66), the distance is still a very long 2046 miles! Whatever distance we calculate for a given frequency is called the wavelength of the signal.

The lower-case Greek letter "lambda" (λ) represents wavelength, in whatever unit of length used in the velocity figure (if miles per second, then wavelength in miles; if meters per second, then wavelength in meters). Velocity of propagation is usually the speed of light when calculating signal wavelength in open air or in a vacuum, but will be less if the transmission line has a velocity factor less than 1.

If a "long" line is considered to be one at least 1/4 wavelength in length, you can see why all connecting lines in the circuits discussed thusfar have been assumed "short." For a 60 Hz AC power system, power lines would have to exceed 775 miles in length before the effects of propagation time became significant. Cables connecting an audio amplifier to speakers would have to be over 4.65 miles in length before line reflections would significantly impact a 10 kHz audio signal!

When dealing with radio-frequency systems, though, transmission line length is far from trivial. Consider a 100 MHz radio signal: its wavelength is a mere 9.8202 feet, even at the full propagation velocity of light (186,000 m/s). A transmission line carrying this signal would not have to be more than about 2-1/2 feet in length to be considered "long!" With a cable velocity factor of 0.66, this critical length shrinks to 1.62 feet.

When an electrical source is connected to a load via a "short" transmission line, the load's impedance dominates the circuit. This is to say, when the line is short, its own characteristic impedance is of little consequence to the circuit's behavior. We see this when testing a coaxial cable with an ohmmeter: the cable reads "open" from center conductor to outer conductor if the cable end is left unterminated. Though the line acts as a resistor for a very brief period of time after the meter is connected (about 50 Ω for an RG-58/U cable), it immediately thereafter behaves as a simple "open circuit:" the impedance of the line's open end. Since the combined response time of an ohmmeter and the human being using it greatly exceeds the round-trip propagation time up and down the cable, it is "electrically short" for this application, and we only register the terminating (load) impedance. It is the extreme speed of the propagated signal that makes us unable to detect the cable's 50 Ω transient impedance with an ohmmeter.

If we use a coaxial cable to conduct a DC voltage or current to a load, and no component in the circuit is capable of measuring or responding quickly enough to "notice" a reflected wave, the cable is considered "electrically short" and its impedance is irrelevant to circuit function. Note how the electrical "shortness" of a cable is relative to the application: in a DC circuit where voltage and current values change slowly, nearly any physical length of cable would be considered "short" from the standpoint of characteristic impedance and reflected waves. Taking the same length of cable, though, and using it to conduct a high-frequency AC signal could result in a vastly different assessment of that cable's "shortness!"

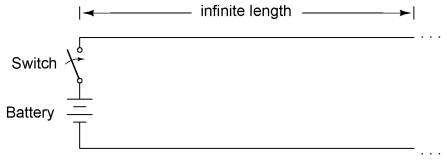
When a source is connected to a load via a "long" transmission line, the line's own characteristic impedance dominates over load impedance in determining circuit behavior. In other words, an electrically "long" line acts as the principal component in the circuit, its own characteristics overshadowing the load's. With a source connected to one end of the cable and a load to the other, current drawn from the source is a function primarily of the line and not the load. This is increasingly true the longer the transmission line is. Consider our hypothetical 50 Ω cable of infinite length, surely the ultimate example of a "long" transmission line: no matter what kind of load we connect to one end of this line, the source (connected to the other end) will only see 50 Ω of impedance, because the line's infinite length prevents the signal from ever reaching the end where the load is connected. In this scenario, line impedance exclusively defines circuit behavior, rendering the load completely irrelevant.

The most effective way to minimize the impact of transmission line length on circuit behavior is to match the line's characteristic impedance to the load impedance. If the load impedance is equal to the line impedance, then anysignal source connected to the other end of the line will "see" the exact same impedance, and will have the exact same amount of current drawn from it, regardless of line length. In this condition of perfect impedance matching, line length only affects the amount of time delay from signal departure at the source to signal arrival at the load. However, perfect matching of line and load impedance is not always practical or possible.

The next section discusses the effects of "long" transmission lines, especially when line length happens to match specific fractions or multiples of signal wavelength.
Review
Coaxial cabling is sometimes used in DC and low-frequency AC circuits as well as in high-frequency circuits, for the excellent immunity to induced "noise" that it provides for signals.

When the period of a transmitted voltage or current signal greatly exceeds the propagation time for a transmission line, the line is considered electrically short. Conversely, when the propagation time is a large fraction or multiple of the signal's period, the line is considered electrically long.

A signal's wavelength is the physical distance it will propagate in the time span of one period.

Wavelength is calculated by the formula λ=v/f, where "λ" is the wavelength, "v" is the propagation velocity, and "f" is the signal frequency.

A rule-of-thumb for transmission line "shortness" is that the line must be at least 1/4 wavelength before it is considered "long."

In a circuit with a "short" line, the terminating (load) impedance dominates circuit behavior. The source effectively sees nothing but the load's impedance, barring any resistive losses in the transmission line.

In a circuit with a "long" line, the line's own characteristic impedance dominates circuit behavior. The ultimate example of this is a transmission line of infinite length: since the signal will never reach the load impedance, the source only "sees" the cable's characteristic impedance.

When a transmission line is terminated by a load precisely matching its impedance, there are no reflected waves and thus no problems with line length.

Read More About

Circuit Schematic Symbols

Transmission line- 50-Ohm Cable- Part-A

Transmission line-Circuits and the speed of light-Part-B

Transmission line-Characteristic impedance-part-c

Finite-length transmission lines-Part-D

Jan 30, 2018

Concept of Wound rotor induction motors

Wound rotor induction motors

A wound rotor induction motor has a stater like the squirrel cage induction motor, but a rotor with insulated winding brought out via slip rings and brushes. However, no power is applied to the slip rings. Their sole purpose is to allow resistance to be placed in series with the rotor winding while starting. This resistance is shorted out once the motor is started to make the rotor look electrically like the squirrel cage counterpart.

Nuclear power plant

A generating station in which nuclear energy is converted into electrical energy is known as a nuclear power station.

CIRCUIT BREAKER AND RELAY

Q. Explain different types of faults?

Free download eBook& tools

A. Free download - eBook

➽ E-BOOK ELECTRICAL

➽ E-BOOK INSTRUMENTATION

➽ E-BOOK AUTOMATION

➽ E-BOOK ENGLISH LEARNING

➽ E-BOOK CHEMICAL

➽ E-BOOK MECHANICAL

➽ E-BOOK MATHEMATICS

➽ E-BOOK PHYSICS

➽ E-BOOK OTHERS

B. Free download - Excel tools

➽ CALCULATION TOOL (EXCEL)

Jan 29, 2018

Synchronous Motors construction and working principal

Synchronous Motors-Part-A

Single phase synchronous motors are available in small sizes for applications requiring precise timing such as time keeping, (clocks) and tape players. Though battery powered quartz regulated clocks are widely available, the AC line operated variety has better long term accuracy-- over a period of months. This is due to power plant operators purposely maintaining the long term accuracy of the frequency of the AC distribution system. If it falls behind by a few cycles, they will make up the lost cycles of AC so that clocks lose no time. Above 10 Horsepower (7.5 kW) the higher efficiency and leading power factor make large synchronous motors useful in industry. Large synchronous motors are a few percent more efficient than the more common induction motors. Though, the synchronous motor is more complex.

Rich Dad Poor Dad

There is a Need Does school prepare children for the real world? “Study hard and get good grades and you will find a high-paying job with great benefits,” my parents used to say. Their goal in life was to provide a college education for my older sister and me, so that we would have the greatest chance for success in life. When I finally earned my diploma in 1976-graduating with honors, and near the top of my class, in accounting from Florida State University-my parents had realized their goal. It was the crowning achievement of their lives. In accordance with the “Master Plan,” I was hired by a “Big 8” accounting firm, and I looked forward to a long career and retirement at an early age.

Instruments transformers and its applications

Special transformers and applications

Because transformers can step voltage and current to different levels, and because power is transferred equivalently between primary and secondary windings, they can be used to "convert" the impedance of a load to a different level. That last phrase deserves some explanation, so let's investigate what it means.

Power measurement

Power measurement in AC circuits can be quite a bit more complex than with DC circuits for the simple reason that phase shift makes complicates the matter beyond multiplying voltage by current figures obtained with meters. What is needed is an instrument able to determine the product (multiplication) of instantaneous voltage and current. Fortunately, the common electrodynamometer movement with its stationary and moving coil does a fine job of this.
Three phase power measurement can be accomplished using two dynamometer movements with a common shaft linking the two moving coils together so that a single pointer registers power on a meter movement scale. This, obviously, makes for a rather expensive and complex movement mechanism, but it is a workable solution. An ingenious method of deriving an electronic power meter (one that generates an electric signal representing power in the system rather than merely move a pointer) is based on the Hall Effect. The Hall Effect is an unusual effect first noticed by E. H. Hall in 1879, whereby a voltage is generated along the width of a current-carrying conductor exposed to a perpendicular

magnetic field
The voltage generated across the width of the flat, rectangular conductor is directly proportional to both the magnitude of the current through it and the strength of the magnetic field. Mathematically, it is a product (multiplication) of these two variables. The amount of "Hall Voltage" produced for any given set of conditions also depends on the type of material used for the flat, rectangular conductor. It has been found that specially prepared "semiconductor" materials produce a greater Hall voltage than do metals, and so modern Hall Effect devices are made of these. It makes sense then that if we were to build a device using a Hall-effect sensor where the current through the conductor was pushed by AC voltage from an external circuit and the magnetic field was set up by a pair or wire coils energized by the current of the AC power circuit, the Hall voltage would be in direct proportion to the multiple of circuit current and voltage. Having no mass to move (unlike an electromechanical movement), this device is able to provide instantaneous power measurement:

Not only will the output voltage of the Hall Effect device be the representation of instantaneous power at any point in time, but it will also be a DC signal! This is because the Hall voltage polarity is dependent upon both the polarity of the magnetic field and the direction of current through the conductor. If both current direction and magnetic field polarity reverses -- as it would ever half-cycle of the AC power -- the output voltage polarity will stay the same. If voltage and current in the power circuit are 90o out of phase (a power factor of zero, meaning no real power delivered to the load), the alternate peaks of Hall device current and magnetic field will never coincide with each other: when one is at its peak, the other will be zero. At those points in time, the Hall output voltage will likewise be zero, being the product (multiplication) of current and magnetic field strength. Between those points in time, the Hall output voltage will fluctuate equally between positive and negative, generating a signal corresponding to the instantaneous absorption and release of power through the reactive load. The net DC output voltage will be zero, indicating zero true power in the circuit. Any phase shift between voltage and current in the power circuit less than 90o will result in a Hall output voltage that oscillates between positive and negative, but spends more time positive than negative. Consequently there will be a net DC output voltage. Conditioned through a low-pass filter circuit, this net DC voltage can be separated from the AC mixed with it, the final output signal registered on a sensitive DC meter movement. Often it is useful to have a meter to totalize power usage over a period of time rather than instantaneously. The output of such a meter can be set in units of Joules, or total energy consumed, since power is a measure of work being done per unit time. Or, more commonly, the output of the meter can be set in units of Watt-Hours. Mechanical means for measuring Watt-Hours are usually cantered around the concept of the motor: build an AC motor that spins at a rate of speed proportional to the instantaneous power in a circuit, then have that motor turn an "odometer" style counting mechanism to keep a running total of energy consumed. The "motor" used in these meters has a rotor made of a thin aluminium disk, with the rotating magnetic field established by sets of coils energized by line voltage and load current so that the rotational speed of the disk is dependent on both voltage and current.
Read Also
Transformer Winding configurations
Basic concept and Calculating of Power Factor
Step-up and step-down transformers
Circuit Schematic Symbols
what is AC commutator motors?
Concept of Brush less DC motor
Concept of Reluctance of motor
Single-phase induction motors concept
Types of specialized motors
Construction & operation of Poly phase motor
What is self synchronous motors?
what is AC commutator motors?
Step-up and step-down transformers
Circuit Schematic Symbols

Finite-length transmission lines-Part-D

Finite-length transmission lines

A transmission line of infinite length is an interesting abstraction, but physically impossible. All transmission lines have some finite length, and as such do not behave precisely the same as an infinite line. If that piece of 50 Ω "RG-58/U" cable I measured with an ohmmeter years ago had been infinitely long, I actually would have been able to measure 50 Ω worth of resistance between the inner and outer conductors. But it was not infinite in length, and so it measured as "open" (infinite resistance).
Nonetheless, the characteristic impedance rating of a transmission line is important even when dealing with limited lengths. An older term for characteristic impedance, which I like for its descriptive value, is surge impedance. If a transient voltage (a "surge") is applied to the end of a transmission line, the line will draw a current proportional to the surge voltage magnitude divided by the line's surge impedance (I=E/Z). This simple, Ohm's Law relationship between current and voltage will hold true for a limited period of time, but not indefinitely.
If the end of a transmission line is open-circuited -- that is, left unconnected the current "wave" propagating down the line's length will have to stop at the end, since electrons cannot flow where there is no continuing path. This abrupt cessation of current at the line's end causes a "pile-up" to occur along the length of the transmission line, as the electrons successively find no place to go. Imagine a train traveling down the track with slack between the rail car couplings: if the lead car suddenly crashes into an immovable barricade, it will come to a stop, causing the one behind it to come to a stop as soon as the first coupling slack is taken up, which causes the next rail car to stop as soon as the next coupling's slack is taken up, and so on until the last rail car stops. The train does not come to a halt together, but rather in sequence from first car to last:

A signal propagating from the source-end of a transmission line to the load-end is called an incident wave. The propagation of a signal from load-end to source-end (such as what happened in this example with current encountering the end of an open-circuited transmission line) is called a reflected wave.
When this electron "pile-up" propagates back to the battery, current at the battery ceases, and the line acts as a simple open circuit. All this happens very quickly for transmission lines of reasonable length, and so an ohmmeter measurement of the line never reveals the brief time period where the line actually behaves as a resistor. For a mile-long cable with a velocity factor of 0.66 (signal propagation velocity is 66% of light speed, or 122,760 miles per second), it takes only 1/122,760 of a second (8.146 microseconds) for a signal to travel from one end to the other. For the current signal to reach the line's end and "reflect" back to the source, the round-trip time is twice this figure, or 16.292 μs.
High-speed measurement instruments are able to detect this transit time from source to line-end and back to source again, and may be used for the purpose of determining a cable's length. This technique may also be used for determining the presence and location of a break in one or both of the cable's conductors, since a current will "reflect" off the wire break just as it will off the end of an open-circuited cable. Instruments designed for such purposes are called time-domain reflectometers (TDRs). The basic principle is identical to that of sonar range-finding: generating a sound pulse and measuring the time it takes for the echo to return.
A similar phenomenon takes place if the end of a transmission line is short-circuited: when the voltage wave-front reaches the end of the line, it is reflected back to the source, because voltage cannot exist between two electrically common points. When this reflected wave reaches the source, the source sees the entire transmission line as a short-circuit. Again, this happens as quickly as the signal can propagate round-trip down and up the transmission line at whatever velocity allowed by the dielectric material between the line's conductors.
A simple experiment illustrates the phenomenon of wave reflection in transmission lines. Take a length of rope by one end and "whip" it with a rapid up-and-down motion of the wrist. A wave may be seen traveling down the rope's length until it dissipates entirely due to friction:

This is analogous to a long transmission line with internal loss: the signal steadily grows weaker as it propagates down the line's length, never reflecting back to the source. However, if the far end of the rope is secured to a solid object at a point prior to the incident wave's total dissipation, a second wave will be reflected back to your hand:

Usually, the purpose of a transmission line is to convey electrical energy from one point to another. Even if the signals are intended for information only, and not to power some significant load device, the ideal situation would be for all of the original signal energy to travel from the source to the load, and then be completely absorbed or dissipated by the load for maximum signal-to-noise ratio. Thus, "loss" along the length of a transmission line is undesirable, as are reflected waves, since reflected energy is energy not delivered to the end device.
Reflections may be eliminated from the transmission line if the load's impedance exactly equals the characteristic ("surge") impedance of the line. For example, a 50 Ω coaxial cable that is either open-circuited or short-circuited will reflect all of the incident energy back to the source. However, if a 50 Ω resistor is connected at the end of the cable, there will be no reflected energy, all signal energy being dissipated by the resistor.
This makes perfect sense if we return to our hypothetical, infinite-length transmission line example. A transmission line of 50 Ω characteristic impedance and infinite length behaves exactly like a 50 Ω resistance as measured from one end. If we cut this line to some finite length, it will behave as a 50 Ω resistor to a constant source of DC voltage for a brief time, but then behave like an open- or a short-circuit, depending on what condition we leave the cut end of the line: open or shorted. However, if we terminate the line with a 50 Ω resistor, the line will once again behave as a 50 Ω resistor, indefinitely: the same as if it were of infinite length again:

In essence, a terminating resistor matching the natural impedance of the transmission line makes the line "appear" infinitely long from the perspective of the source, because a resistor has the ability to eternally dissipate energy in the same way a transmission line of infinite length is able to eternally absorb energy.
Reflected waves will also manifest if the terminating resistance isn't precisely equal to the characteristic impedance of the transmission line, not just if the line is left unconnected (open) or jumpered (shorted). Though the energy reflection will not be total with a terminating impedance of slight mismatch, it will be partial. This happens whether or not the terminating resistance is greater or less than the line's characteristic impedance.
Re-reflections of a reflected wave may also occur at the source end of a transmission line, if the source's internal impedance (Thevenin equivalent impedance) is not exactly equal to the line's characteristic impedance. A reflected wave returning back to the source will be dissipated entirely if the source impedance matches the line's, but will be reflected back toward the line end like another incident wave, at least partially, if the source impedance does not match the line. This type of reflection may be particularly troublesome, as it makes it appear that the source has transmitted another pulse.

Review
Characteristic impedance is also known as surge impedance, due to the temporarily resistive behavior of any length transmission line.
A finite-length transmission line will appear to a DC voltage source as a constant resistance for some short time, then as whatever impedance the line is terminated with. Therefore, an open-ended cable simply reads "open" when measured with an ohmmeter, and "shorted" when its end is short-circuited.
A transient ("surge") signal applied to one end of an open-ended or short-circuited transmission line will "reflect" off the far end of the line as a secondary wave. A signal traveling on a transmission line from source to load is called an incident wave; a signal "bounced" off the end of a transmission line, traveling from load to source, is called a reflected wave.
Reflected waves will also appear in transmission lines terminated by resistors not precisely matching the characteristic impedance.
A finite-length transmission line may be made to appear infinite in length if terminated by a resistor of equal value to the line's characteristic impedance. This eliminates all signal reflections.
A reflected wave may become re-reflected off the source-end of a transmission line if the source's internal impedance does not match the line's characteristic impedance. This re-reflected wave will appear, of course, like another pulse signal transmitted from the source.

Transmission line- 50-Ohm Cable- Part-A

Transmission line-Circuits and the speed of light-Part-B

Transmission line-Characteristic impedance-part-c

Synchronous Motors construction and working principal PART-B

Brush less DC motor- Synchronous Motors-PART-B

Brushless DC motors were developed from conventional brushed DC motors with the availability of solid state power semiconductors. So, why do we discuss brushless DC motors in a chapter on AC motors? Brushless DC motors are similar to AC synchronous motors. The major difference is that synchronous motors develop a sinusoidal back EMF, as compared to a rectangular, or trapezoidal, back EMF for brushless DC motors. Both have stator created rotating magnetic fields producing torque in a magnetic rotor.

Winding configurations

Transformers are very versatile devices. The basic concept of energy transfer between mutual inductors is useful enough between a single primary and single secondary coil, but transformers don't have to be made with just two sets of windings. Consider this transformer circuit:

Reluctance motor

The variable reluctance motor is based on the principle that an unrestrained piece of iron will move to complete a magnetic flux path with minimum reluctance, the magnetic analog of electrical resistance.

Characteristic impedance

Suppose, though, that we had a set of parallel wires of infinite length, with no lamp at the end. What would happen when we close the switch? Being that there is no longer a load at the end of the wires, this circuit is open. Would there be no current at all?

Main Menu